公式的目的是要从另外一个角度重现传统MACD,以便有一些不同于传统的解释角度。但我发现全文的基础,所谓的K线定律,其实是错误的。见凌见在一开头指出了要证明的结果:
DIF=(LONG-SHORT)/2*EMA(EMA((C-REF(C,1)),SHORT),LONG)
=((LONG-SHORT)/2)*EMA(EMA(C,SHORT)-REF(EMA(C,SHORT),1),LONG)
=EMA(C,SHORT)-EMA(C,LONG)
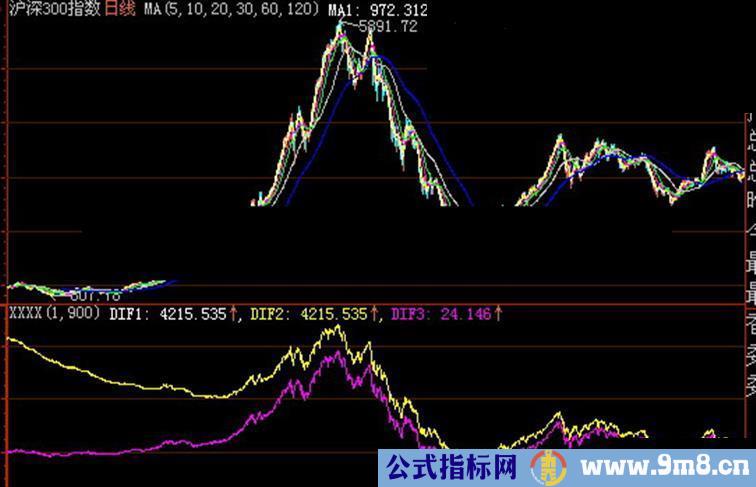
事实上,最后一个等式不成立。犯错的原因在于只通过软件里面的图线来证明等式,而没有从数学上进行严格证明。从具体图线表现来看,也很容易证明楼主的等式不成立。下面是见凌见版本的MACD大智慧的公式,我只是加上了三个变量名称DIF,DIF2,DIF3,和参数命令行。直接拷贝到软件里就可以使用:
{公式名称:XXXX,副图}
INPUT: SHORT(5,1,900),LONG(30,1,900);
DIF1: (LONG-SHORT)/2*EMA(EMA((C-REF(C,1)),SHORT),LONG);
DIF2: ((LONG-SHORT)/2)*EMA(EMA(C,SHORT)-REF(EMA(C,SHORT),1),LONG);
DIF3: EMA(C,SHORT)-EMA(C,LONG) ;
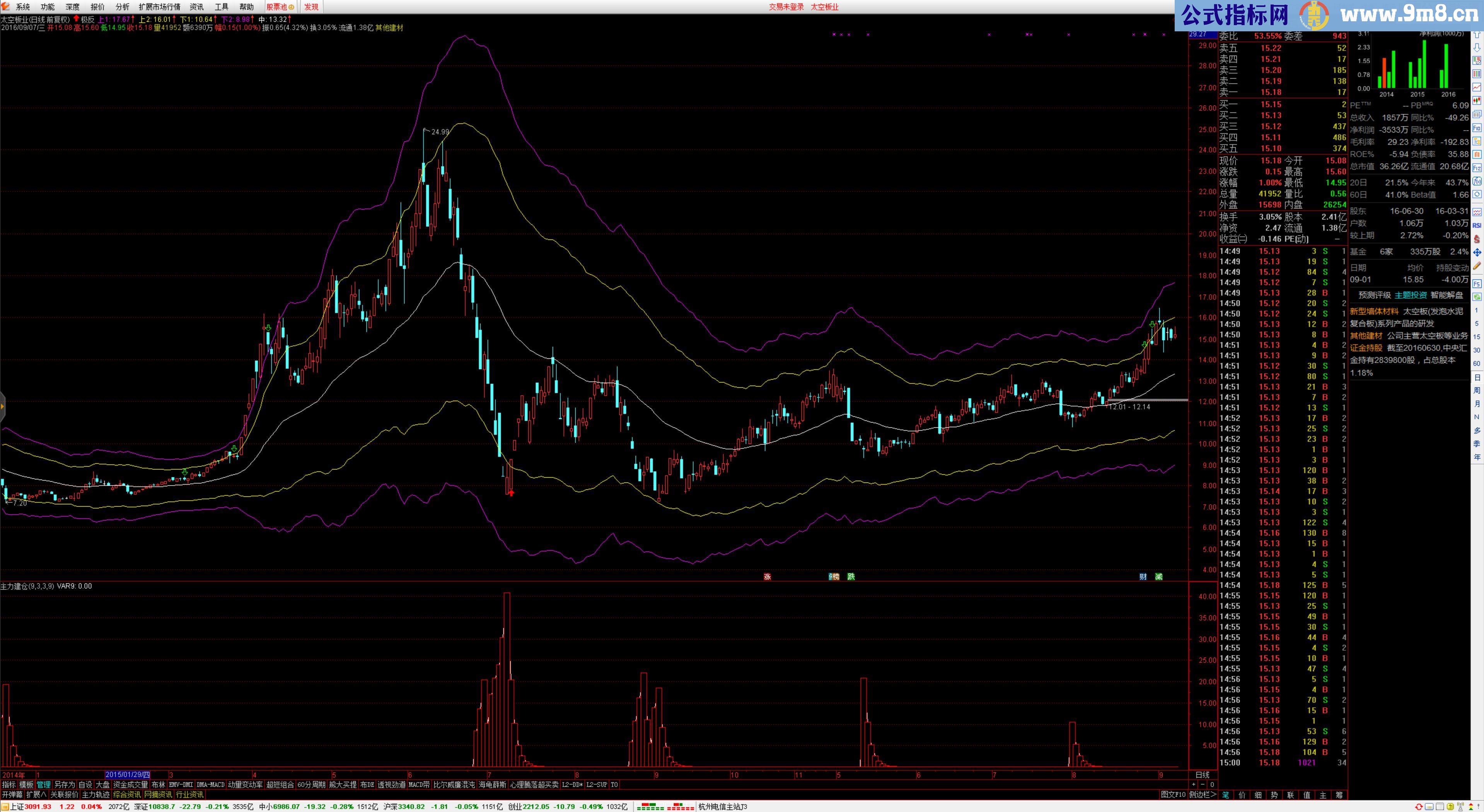
DIF1=DIF2,这个是可以严格证明的。因此图线上看应该不会多于2条线。当SHORT和LONG差别不是太大的话,肉眼只看到1条线,应该是电脑计算精度所限,基本相等。如果两个参数差别很大的话,例如SHORT=1,LONG=900,则DIF1和DIF3两条曲线的差别很大。详见下面图示。
因此,可以肯定,见凌见原文中提出的所谓的相等,不是数学上相等,只是数值计算结果在一定条件下近似相等。从数学角度看,这个K线微积分定律并不存在。至于DIF2能做什么事情,确实值得进一步讨论。