定义:离散系数,离散系数又称变异系数,是统计学当中的常用统计指标,主要用于比较不同水平的变量数列的离散程度及平均数的代表性。
引用网上的一个例子说明 平均值、标准差和离散系数。
假设存在A、B两组数据,A组为{1、4、7、10},B组{4、5、6、7},通过计算,我们不难得出A、B两组数据的平均值都是5.5。平均值有什么意义呢?它反映数据的中心点。上述A、B两组数据的中心点都在5.5这个位置。我们再进一步观察不难发现另一个有趣的问题——A组数据基本远离平均值,而B组数据基本围绕在平均值附近。那么这种距离平均值的远近用什么来度量呢?统计学上引入了“标准差”概念,标准差越趋近于0,说明数据的分散性越小,集中性越理想。通过计算,我们得出A组的标准差为6.71,B组的标准差为2.25。说明B组分散性小于A组,B组集中性优于A组。由于数值动态变化现象极其复杂,标准差的大小难于准确表达数值的分散程度,因此统计学上又引入另一个概念——“离散系数”,离散系数=标准差/平均值。离散系数越小,数据集中性越优。上述A组数据的离散系数为6.71/5.5=1.22,B组数据的离散系数为:2.25/5.5=0.41。到此,不用说你也看出上述A、B两组数字的集中性、离散性的优劣了——B组数据的离散系数远小于A组数据,B组数据的集中性明显优于A组。
上述统计学知识与离散系数与股票有何相关呢?经研究,探索、发现三个重要现象:
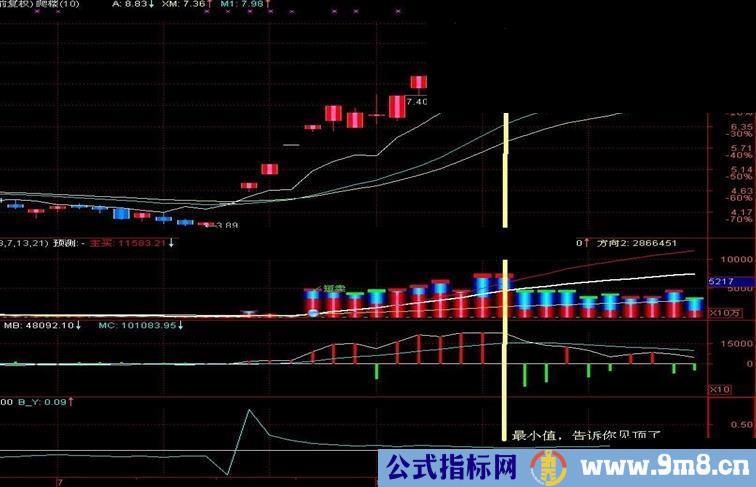
1、股票的运行总是呈非线性的波段周期运动——设动态离散系数为X,当X从(-∞<X<0,0>X>-∞)区间的最高值发展到(∞>X>0,0<X<∞)区间的最低值时,股价完成一个波段上涨运动。当X从(∞>X>0,0<X<∞)区间的最低值发展到(-∞<X<0,0>X>-∞)区间的最高值时,股价完成一个波段下跌运动。上述两者结合起来,就组成股票的一个非线性波段周期。每只股票都存在这样的周期,只是周期大小、长短的不同(即非线性)。
2、离散系数X位于(-∞<X<0,0>X>-∞)区间的运行轨迹呈开口朝下的抛物线,存在着一个最大值。当X为最大值时,股价存在一个最佳的波段底部,当离散系数从该最大值变小,比如前天-0.42,昨天-0.30,今天-0.39,它告诉你明天是买进的时候了。
3、离散系数X位于(∞>X>0,0<X<∞)区间的运行轨迹呈开口朝上的抛物线,存在着一个最小值。当X为最小值时,股价趋于上涨最佳状态,特别是该最小值趋近于0(比如0.08、0.15等等)时,股价会出现巨幅拉升,甚至出现涨停板。当X从该最小值变大如前天0.42,昨天0.30,今天0.39,它告诉你,明天是出货的时候了。
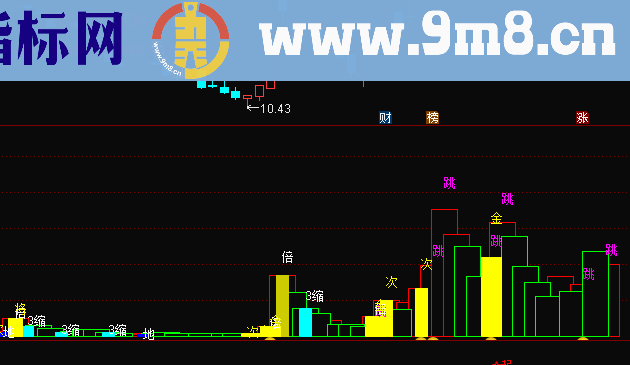
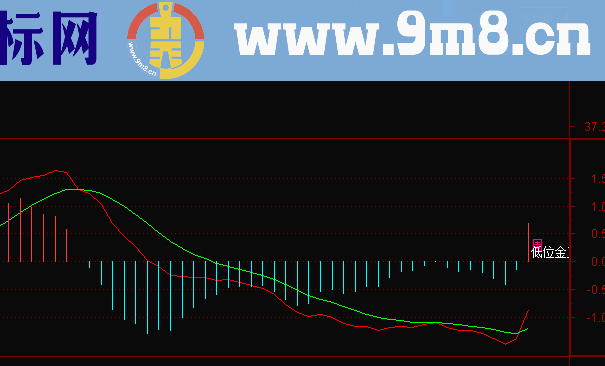
示意图: