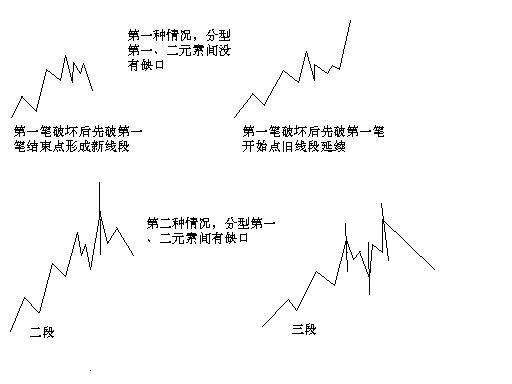
虽然67课已经给出了线段划分的标准,但由于那里用的是比较抽象的类数学语言,所以理解上可能还有困难,因此,逐一进行再分辨。
首先要分辨的,是特征序列中元素的包含关系。注意,特征序列的元素包含关系,首先的前提是这元素都在一特征序列里,如果两个不同的特征序列之间的元素,讨论包含关系是没意义的。显然,特征序列的元素的方向,和其对应的段的方向是刚好相反的,例如,一个向上段后接着一个向下段,前者的特征序列元素是向下的,后者是向上的,因此,根本也不可能存在包含的可能。
那么,为什么可以定义特征序列的分型呢?因为在实际判断中,在前一段没有被笔破坏时,依然不能定义后特征序列的元素,这时候,当然可以存在前一特征序列的分型,这时候,由于还在同一特征序列中,因此,序列元素的包含关系是可以成立的;而当前一段被笔破坏时,显然,最早破坏的一笔如果不是转折点开始的第一笔,那么,特征序列的分型结构也能成立,因为在这种情况下,转折点前的最后一个特征序列元素与转折点后第一个特征元素之间肯定有缺口,而且后者与最早破坏那笔肯定不是包含关系,否则该缺口就不可能被封闭,破坏那笔也就不可能破坏前一线段的走势。这里的逻辑关系很明确的,线段要被笔破坏,那么必须其最后一个特征序列的缺口被封闭,否则就不存在被笔破坏的情况。
那么,现在只剩下最后一种情况,就是最早破坏那笔就是转折点下来的第一笔,这种情况下,这一笔,如果后面延伸出成为线段的走势,那么这一笔就属于中间地带,既不能说是前面一段的特征序列,更不能说是后一段的特征序列,在这里情况下,即使出现似乎有特征序列的包含关系的走势,也不能算,因为,这一笔不是严格地属于前一段的特征序列,属于待定状态,一旦该笔延伸出三笔以上,那么新的线段就形成了,那时候谈论前一线段特征序列的包含关系就没意义了。
总之,上面说得很复杂,其实就是一句话,特征序列的元素要探讨包含关系,首先必须是同一特征序列的元素,这在理论上十分明确的。
从上面的分析就可以知道,从转折点开始,如果第一笔就破坏了前线段,进而该笔延伸出三笔来,其中第三笔破点第一笔的结束位置,那么,新的线段一定形成,前线段一定结束。
这种情况还有更复杂一点的情况,就是第三笔完全在第一笔的范围内,这样,这三笔就分不出是向上还是向下,这样也就定义不了什么特征序列,为什么?因为特征序列是和走势相反的,而走势连方向都没有,那怎么知道哪个元素属于特征序列?这种情况,无非两种最后的结果:1、最终还是先破了第一笔的结束位置,这时候,新的线段显然成立,旧线段还是被破坏了;2、最终,先破第一笔的开始位置,这样,旧线段只被一笔破坏,接着就延续原来的方向,那么,显然旧线段依然延续,新线段没有出现。
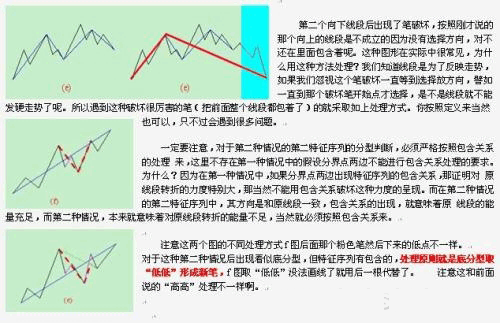
在67课里,把线段的划分分为两种情况,显然,分清楚是哪种情况,对划分线段十分关键。其实,在那里已经把问题说得很清楚,判断的标准只有一个,就是特征序列的分型中,第一和第二元素间不存在特征序列的缺口。从上面的分析可以知道,这个分型结构中所谓特征序列的元素,其实是站在假设旧线段没被破坏的角度说的,而就像所有的分型一样,就算是一般K线的,都是前后两段走势的分水岭、连接点。这和包含的情况不同,包含的关系是对同一段说的,而分型,必然是属于前后的,这时候,在构成分型的元素里,如果线段被最终破坏,那后面的元素肯定不是特征序列里的,也就是说,这时候,分型右侧的元素肯定不属于前后任何一段的特征序列。
这个道理其实很明白,例如前一段是向上的,那么特征序列元素是向下的,而在顶分型的右侧元素,如果最终真满足破坏前线段的要求,那么后线段的方向就是向下的,其特征序列就是向上的,而顶分型的右侧元素是向下的,显然不属于后一段的特征元素,而该顶分型的右侧元素又属于后一段,那么显然更不是前一段的特征元素。所以,对于顶分型的右侧特征元素,只是一般判断方面的一种方便的预设,就如同几何里面,添加辅助线去证明问题一样,辅助线不属于图形本身,就如同顶分型的右侧特征元素其实不一定属于任何的特征元素,但对研究有帮助,当然是要大力去用的,如此而已。
其实,线段的划分,都是可以当下完成的,无非是如下的程序:假设某转折点是两线段的分界点,然后对此用线段划分的两种情况去考察是否满足,如果满足其中一种,那么这点就是真正的线段的分界点;如果不满足,那就不是,原来的线段依然延续,就这么简单。
特征序列的分型中,第一元素就是以该假设转折点前线段的最后一个特征元素,第二个元素,就是从这转折点开始的第一笔,显然,这两者之间是同方向的,因此,如果这两者之间有缺口,那么就是第二种情况,否则就是第一种,然后根据定义来考察就可以。
这里还要强调一下包含的问题,上面的分析知道,在这假设的转折点前后那两元素,是不存在包含关系的,因为,这两者已经被假设不是同一性质的东西,不一定是同一特征序列的;但假设的转折点后的顶分型的元素,是可以应用包含关系的。为什么?因此,这些元素间,肯定是同一性质的东西,或者就是原线段的延续,那么就同是原线段的特征序列中,或者就是新线段的非特征序列中,反正都是同一类的东西,同一类的东西,当然可以考察包含关系。
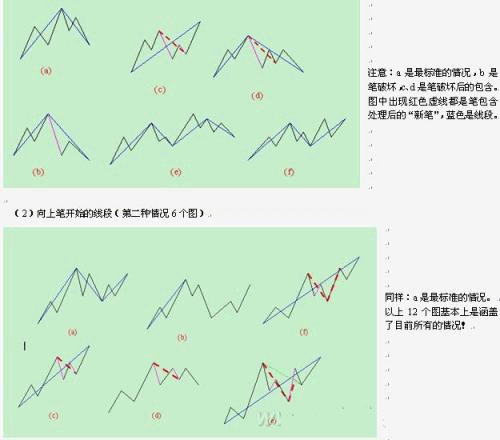
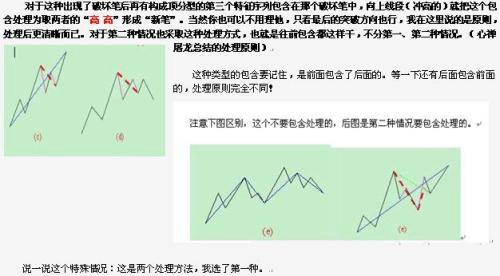
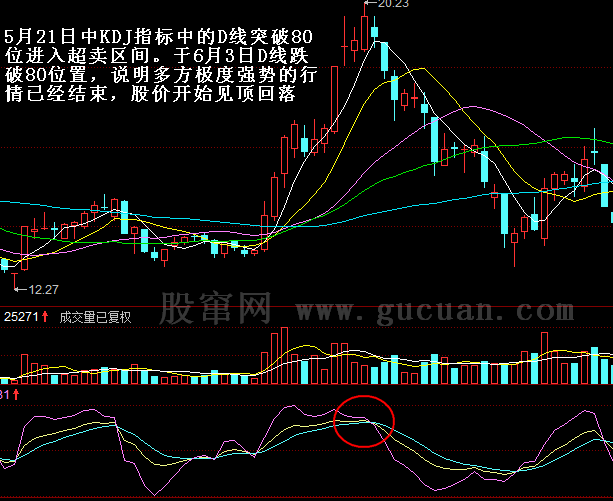
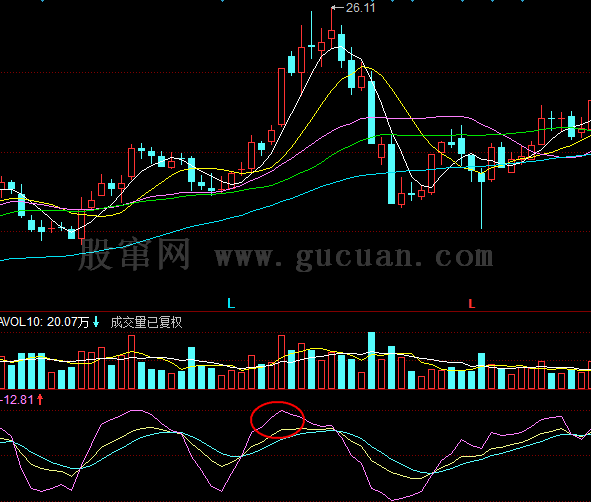
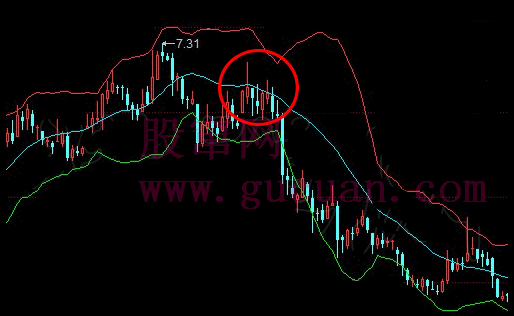
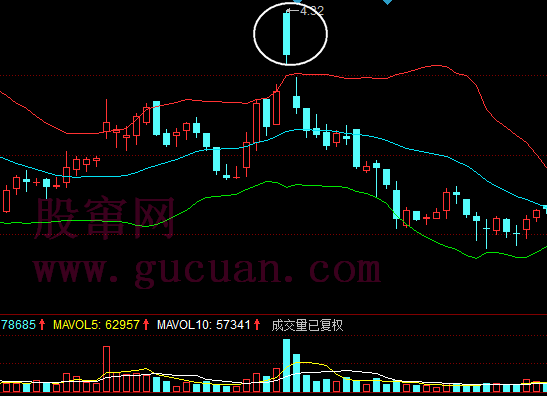
估计看了上面的话,很多人更晕了。下面有几个图,各位可以仔细揣摩一下。但最好还是习惯从定义出发。另外,大盘网友问到的那个图,显然,根据定义,是两个线段,而今天42-44的分段,显然也是成立的。
注意,下图最后一个有问题,请看课程81里的更正说明。